Generative AI and large language models (LLMs)¶
This module is designed to give some overview of and develop our skills in computational tools which may aid our mathematical investigations. It would, therefore, be remiss not to discuss the relative new kids on the block that are AI (artificial intelligence) and ML (machine learning).
AI/ML have developed at an incredible pace in recent years and are now influencing our lives in countless ways, from self-driving cars to disease detection and more.
While the developement of the AI algorithms themselves is a highly mathematical endevour, they have also had a significant impact on mathematical and statistical research more generally, seeing use in 'predicting' chaos, ecological modelling and in compuational algebra.
Where you might be most interested in the use of AI, as a student navigating a mathematics degree, is as a teaching and learning aid.
IMPORTANT¶
It should be said from the outset that unauthorised use of AI when completing assessments is forbidden in the university regulations. This means unless otherwise explicitly stated in the assessment instructions (see tutorial 4), you should not use any AI tool like ChatGPT (see below).
Generally, good practice is to use it only in a responsible way to enhance your understanding of a topic, not as a means to get an answer to a problem. In fact, as we will see, ChatGPT often performs poorly with specific problems but can peform well at regurgitating theory.
This being said, employers will increasingly be expecting students to be aware of AI's abilities, shortcomings and be effective users. This section of the module is designed, in part, to address this.
What is AI?¶
Before launching into a discussion on the pros and cons of popular AI tools we should mention what AI is. This isn't a course in AI, but we can point out the basics for anybody unfamiliar with what it is.
AI is a broad and rather nebulous term covering a range of technologies where an algorithm has been "trained" to be able to perform certain tasks.
Often the underlying algorithm is a neural network, which is essentially a function (with inputs and outputs) that operates on the inputs via layers of neurons. Neurons simply peform a weighted sum of the inputs, the learning part comes when determining what the weights need to be for a specific set of "training data". An optimisation step occurs to set these weights based on finding the minimum of some loss function between the network output and the training data. Other elements are added into the design of the network (number of layers, activation functions, biases etc.) but this is the general idea. A "test" step follows, once the network is trained, to make sure that it is performing correctly. See here for a "worked example".
Generative AI is a class of AI models capable of creating completely new outputs with similar features to the training data. For instance chatbots, which can converse with a user (see below), or text-to-image generators (DALL-E, Stable Diffusion).
What is an LLM?¶
ChatGPT, Bard and Gemini are examples of large language models (LLMs). These are AI trained on very large data sets of text and are designed to emulate human language by producing outputs as "natural language". The idea is to provide a user friendly "chatbot" interface for a back catalogue of human knowledge.
The LLM creates a response based on weighted probabilities; it essentially provides you with an answer which is "most likely" correct or helpful. This means that the LLM can give incorrect or unhelpful answers since these were deemed the "least worst" response. Responses like 'I don't know the answer' are down-weighted significantly. This becomes a significant concern, particularly in fields like mathematics, where precision is crucial, and an incorrect answer is of little use.
This means that the model lacks true 'reasoning' capabilities. While it may appear to present a logical sequence of arguments, this is still a result of the 'least worst' mindset, and the model's responses are essentially educated guesses based on the patterns observed in the training data. If the specific example provided is not present in the training data, the model's accuracy becomes uncertain.
The best use case for us is perhaps to use LLMs to summarise a "textbook" concept, rather than expecting it to complete worked examples for us. For instance, we might ask it to explain what a neural network is (try this as homework!), or remind us of a simple mathematical definition (see below). Keep in mind that you should cross check anything produced by a chatbot in this context, as it can simply make things up, see for instance controversy about made up references, or this dodgy proof. We'll take a look at some more examples below.
It is worth noting at this point in the discussion that the AI is constantly being exposed to new training data and plugged into other computational engines (e.g. Wolfram) so in some circumstances it will be able to query some symbolic computing package to perform mathematical manipulations. This, in some sense, indicates that there are usually more appropriate computational tools for many advanced mathematical applications (e.g. Mathematica, Maple, or a specific computational module/library e.g. GAP or LAPACK).
Examples¶
In this section we will generate some examples using ChatGPT to demonstrate where it can be helpful and where it does a bad job.
We show examples via screenshot. These tools are constantly being re-trained so there is no gaurantee that the prompts used below will give the same response in a few months time (try this!). We've tried to pick out examples to demonstrate the way LLMs work, rather than specific topics that always perform well or not.
Problem cases¶
As we mentioned earlier, specific examples are generally not handled well by LLMs. Often (although increasingly less) the AI will be unable to step you through a complex set of deductions as the example, or similar enough examples, have not been processed in the training data. Similarly the AI does not like to admit defeat and say it does not know the answer or cannot provide an accurate solution; such outcomes are downweighted in the training.
Simple examples can be handled pretty well, for instance solving quadratic equations, performing simple integration and so on. The issue is that you need to be able to verify that a mistake has not been made!
Here is an example where we ask for a solution to a very common ordinary differential equation
$$ y''(x) = -\sin(y), $$which describes the motion of a simple pendulum ($y$ would be the angle made with the vertical and $x$ time), which is well-known to have no closed-form solution, here is what happened

while this might be a worthwhile approach in some examples, it doesn't get us very far with the pendulum and the output suggests that it will. After some more steps which we omit the output gives

This final expression is sometimes used as means to approximate the period of the pendulum. The AI has recognised the solution is not easily obtained but it has not recognised the problem for what it is and that plenty of references, including wikipedia, will give a clearer response and historical context about this equation. Part of the difficulty might be that the variables used are different from the standard notation for the pendulum ($\theta(t)$ instead of $y(x)$).
Note in this example Gemini gave the following as part of its response: The differential equation $y'' = -\sin(y)$ is a nonlinear second-order ordinary differential equation. It describes the motion of a simple pendulum. There's no closed-form analytical solution in terms of elementary functions for general initial conditions.
There are plenty of examples of AI going wrong with elementary mathematical deductions too, for instance:
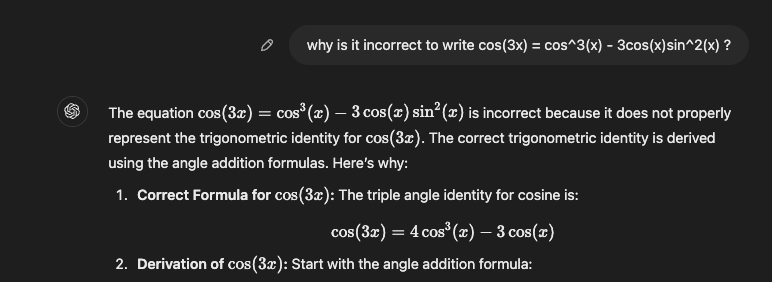
We were a bit cheeky giving the leading question, but most mathematicians would work on the problem and then decide whether the identity is correct, the AI compares to its nearest most common equation for $\cos(3x)$ and then decides there is a mistake.
If we follow up with a different question, the AI does eventually figure it out, but not after some confusing output.


For code?¶
A common use-case for AI is actually in producing code. Some platforms embed a kind of auto-complete system to help, but tools like ChatGPT and Gemini can produce Python code. In a similar way that we have already discussed, we should be prepared to critically evaluate the code, as we would with any other AI output.
Here is an interesting case, ChatGPT was asked
In Python can you write a function is_heterogram which takes a string as input and returns True if it contains no repeated letters (and False otherwise)?
Here is the verbatim output.
def is_heterogram(s):
"""
Checks if the input string is a heterogram (contains no repeated letters).
Parameters:
- s: Input string
Returns:
- True if the string is a heterogram, False otherwise.
"""
s = s.lower() # Make the string case-insensitive
seen = set() # Use a set to track letters
for char in s:
if char.isalpha(): # Only consider letters
if char in seen:
return False # Found a repeated letter
seen.add(char)
return True
# Example usage
if __name__ == "__main__":
print(is_heterogram("The quick brown fox")) # Should return True
print(is_heterogram("hello")) # Should return False
False False
Take some time to digest the code. It turns out the function works perfectly well, however the first example is incorrectly commented, it is also False; both contain repeated letters! Another good example of AI struggling with specifics, a good validation should include both outcomes. See below, functionally the code is correct.
print(is_heterogram("The quick fox"))
print(is_heterogram("abcdefghijklmnopqrstuvwxyz"))
print(is_heterogram("a"))
print(is_heterogram("aa"))
True True True False
On the other hand, casting a critical eye over this code you might realise the approach taken is a little long-winded and somewhat inelegant. If you took MT1003 in recent years you may recognise this example from one of the computing worksheets when discussing Python sets; there we realised a simple way to do this is by conversion to a set and check equality of the length of the raw string and the converted set:
def is_heterogram_sets(s):
s = s.lower().replace(' ', '') # remove case sensitivity and spaces
return len(set(s)) == len(s)
print(is_heterogram_sets("The quick fox"))
print(is_heterogram_sets("abcdefghijklmnopqrstuvwxyz"))
print(is_heterogram_sets("a"))
print(is_heterogram_sets("aa"))
True True True False
%timeit is_heterogram("abcdefghijklmnopqrstuvwxyz")
%timeit is_heterogram_sets("abcdefghijklmnopqrstuvwxyz")
1.2 µs ± 3.72 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each) 465 ns ± 2.17 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
Hopefully you can see that this approach is much simpler. A working code need not be a good code, and good knowledge of programming structures/methods can be extremely helpful.
Here is another more reasonable example where we asked for some code to evaluate the trapezium rule for numerical integration:
def trapezoidal_rule_integral(f, a, b, n):
"""
Compute the definite integral of a function using the trapezoidal rule.
Parameters:
- f: The function to be integrated.
- a: The lower limit of integration.
- b: The upper limit of integration.
- n: The number of subintervals.
Returns:
The approximate value of the definite integral.
"""
h = (b - a) / n
result = 0.5 * (f(a) + f(b))
for i in range(1, n):
result += f(a + i * h)
result *= h
return result
# Example usage: Compute the indefinite integral of x^2 from 0 to 1
def function_to_integrate(x):
return x**2
lower_limit = 0
upper_limit = 1
num_subintervals = 1000
result = trapezoidal_rule_integral(function_to_integrate, lower_limit, upper_limit, num_subintervals)
print(f"The approximate integral is: {result}")
The approximate integral is: 0.33333349999999995
The code looks good and obeys a number of the good practice principles that we have discussed earlier. There is even a validation example provided linking back to our discussion on computational thinking.
However, we know from our good practice discussion that Python can conduct numerical operations like these ones much more quickly by using vectorisation via numpy arrays. Adding into the prompt "using numpy arrays" yields the following code:
import numpy as np
def trapezoidal_rule_integral2(f, a, b, n):
"""
Compute the definite integral of a function using the trapezoidal rule.
Parameters:
- f: The function to be integrated.
- a: The lower limit of integration.
- b: The upper limit of integration.
- n: The number of subintervals.
Returns:
The approximate value of the definite integral.
"""
x_values = np.linspace(a, b, n + 1)
h = (b - a) / n
result = 0.5 * (f(a) + f(b)) + np.sum(f(x_values[1:-1]))
result *= h
return result
# Example usage: Compute the indefinite integral of x^2 from 0 to 1 using NumPy arrays
def function_to_integrate(x):
return x**2
lower_limit = 0
upper_limit = 1
num_subintervals = 1000
result = trapezoidal_rule_integral2(function_to_integrate, lower_limit, upper_limit, num_subintervals)
print(f"The approximate integral is: {result}")
The approximate integral is: 0.33333349999999995
%timeit trapezoidal_rule_integral(function_to_integrate, lower_limit, upper_limit, num_subintervals)
%timeit trapezoidal_rule_integral2(function_to_integrate, lower_limit, upper_limit, num_subintervals)
92.1 µs ± 651 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each) 8.17 µs ± 67.1 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
We get the same result but now much more efficiently. The key with this example is knowing the best prompt to give ChatGPT, there is significant danger in using it naively and expecting good quality code.
"That's textbook"¶
Arguably the best thing to use an LLM for is to revise/refresh simple bookwork results where the chatbot will just parrot a standard definition widely found in multiple sources. In this sense we use them like we would any other reference material like an internet search, a textbook or the lecture notes for your modules. You may even notice the wording of a standard definition from an LLM follows closely some prominent source like wikipedia because this is in the training data. Importantly for your studies you should always consider the lecture notes or course materials the definitive source; this should be thought of as your training data!
Here are a few examples of potentially helpful interactions with ChatGPT:


The first two examples are quite standard. The third one on Fourier Series is textbook stuff too, however when you learn Fourier Series as a mathematician you will learn how the coefficients are obtained by these formulas and what properties of the Fourier basis functions are important. This is really very valuable for a good understanding of Fourier Series and the ChatGPT definition is missing it. One could give further prompts to get this information but you need to know what is missing, so just be wary.
Report writing
If you read into LLMs more widely you may notice that they are often used for language correction, proof-reading or to improve/edit text generally. For mathematicians this can be useful when we come to write journal articles or when you are report writing, however, as we mentioned at the beginning the university forbids this usage and language correction should only be used where authorised and acknowledged. The same reasoning applied here as to the mathematical use of AI; if we are unable to write effectively ourselves, how do we know the AI is performing well?
One thing that you might find useful, when it comes to writing dissertations or reports, is a quick way to obtain standard $\LaTeX$ code. When I asked
can you give me the LaTeX code for the incompressible Navier-Stokes equations?
to ChatGPT I got
\begin{align}
\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} &= -\nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{f}, \\
\nabla \cdot \mathbf{u} &= 0,
\end{align}
where:
\begin{itemize}
\item $\mathbf{u}$ is the velocity vector field,
\item $t$ is time,
\item $p$ is the pressure field,
\item $\nu$ is the kinematic viscosity,
\item $\mathbf{f}$ represents external forces (e.g., gravity),
\item $\nabla$ denotes the gradient operator,
\item $\nabla \cdot$ represents the divergence operator,
\item $\nabla^2$ is the Laplacian operator.
\end{itemize}
which renders as
\begin{align} \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} &= -\nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{f}, \\ \nabla \cdot \mathbf{u} &= 0, \end{align}where:
- $\mathbf{u}$ is the velocity vector field,
- $t$ is time,
- $p$ is the pressure field,
- $\nu$ is the kinematic viscosity,
- $\mathbf{f}$ represents external forces (e.g., gravity),
- $\nabla$ denotes the gradient operator,
- $\nabla \cdot$ represents the divergence operator,
- $\nabla^2$ is the Laplacian operator.
which might be quicker than typing it out yourself if you are new to writing $\LaTeX.$